复合函数
函数的复合(Composition):
函数和
的复合:
,可以理解为首先将
输入给函数
获得输出
后将其进而输入给函数
,最终获得结果
。
- 几个函数的复合结果仍然是一个函数:接受输入,给出输出
- 任何函数都可以看成是若干个函数的复合
的定义域与
的定义域相同,但值域不一定与
的值域相同。
例如:,函数
可以视为
和
复合后的结果。
的值域为
,但
的值域为
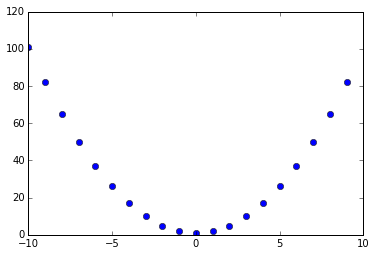
在Python中我们可以很直观地对函数进行复合:
def f(x): return x+1
def g(x): return x**2
def h(x): return f(g(x))
x = np.array(range(-10,10))
# 这里我们使用了Python的list comprehension来计算y
y = np.array([h(i) for i in x])
# 'bo' 将表示我们会使用蓝色的圆圈绘制点图,而非默认的线图
plt.plot(x, y, 'bo')
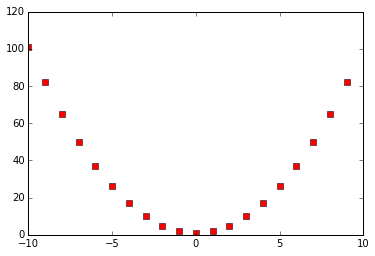
我们也可以使用Python的lambda函数功能来简明地定义:
h2 = lambda x: f(g(x))
plt.plot(x,h2(x),'rs')
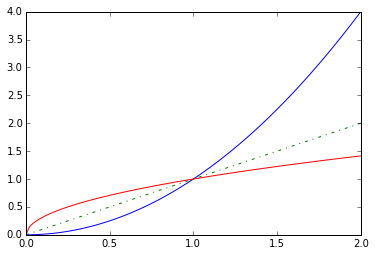
逆函数(Inverse Function):
给定一个函数,其逆函数
是一个与
进行复合后会得到
的特殊函数。
函数与其反函数的函数图一定是关于直线对称的:
w = lambda x: x**2
winv = lambda x: sqrt(x)
x = np.linspace(0,2,100)
plt.plot(x, w(x),'b',x,winv(x),'r',x,x,'g-.')
高阶函数(Higher Order Functions):
我们可以不局限于仅将数值作为函数的输入输出,函数本身也可以作为输入和输出。
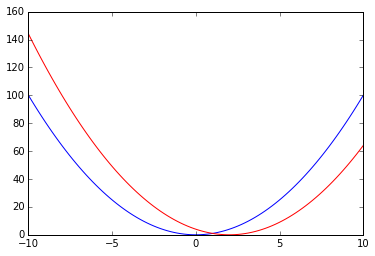
def horizontal_shift(f,H): return lambda x: f(x-H)
上面定义的函数,接受的输入是一个函数
个一个实数
,而输出是一个新的函数,新函数是将
沿着水平方向平移了距离
后得到的。
x = np.linspace(-10,10,100)
shifted_g = horizontal_shift(g,2)
plt.plot(x,g(x),'b',x,shifted_g(x),'r')
以高阶函数的观点看去,函数的复合便是将两个函数作为输入给复合函数,然后由其产生一个新的函数作为输出。复合函数可以如此定义:
def composite(f,g): return lambda x: f(g(x))
h3 = composite(f,g)
print sum(h(x)==h3(x))==len(x)
# result: True