优化
高阶导数(Higher Derivatives)
高阶导数的递归式定义为:
函数的
阶导数
(或记为
)为:
如果将求导数看作是一个运算符,则相当于反复对运算的结果使用
次运算符:
from sympy.abc import x
from sympy.abc import y
f = x**2*y-2*x*y
# 求关于x的二次导数
print f.diff(x,2)
# result : 2*y
# 等同于反复关于x求两次导数
print f.diff(x).diff(x)
# result : 2*y
# 先求关于x的导数,再求关于y的导数,这个该怎么解读?
print f.diff(x,y)
# result : 2*(x - 1)
优化问题(Optimization Problem)
很多时候,我们用函数来描述我们关心的问题,例如:
plt.figure(1, figsize=(4,4))
plt.axis('off')
plt.axhspan(0,1,0.2,0.8,ec = "none")
plt.axhspan(0.2,0.8,0,0.2,ec = "none")
plt.axhspan(0.2,0.8,0.8,1,ec = "none")
plt.axhline(0.2,0.2,0.8,linewidth = 2, color = 'black')
plt.axvline(0.2,0.17,0.23,linewidth = 2, color = 'black')
plt.axvline(0.8,0.17,0.23,linewidth = 2, color = 'black')
plt.axvline(0.2,0.8,1,linewidth = 2, color = 'black')
plt.axhline(0.8,0.17,0.23,linewidth = 2, color = 'black')
plt.axhline(1,0.17,0.23,linewidth = 2, color = 'black')
plt.text(0.495,0.22,r"$l$", fontsize = 18,color="black")
plt.text(0.1,0.9,r"$\frac{4-l}{2}$", fontsize = 18,color="black")
plt.show()

用一张给定边长的正方形纸来折一个没有盖的纸盒,设纸盒的底部边长为
,纸盒的高为
,那么纸盒的体积为:
我们会希望知道怎样才能使得纸盒的容积最大,也就是关心在,的限制条件下,函数
的最大值是多少。
优化问题关心的就是这样的问题,在满足限制条件的前提之下,怎样能够使我们的目标函数最大(或最小)。
l = np.linspace(0,4,100)
V = lambda l: 0.5*l**2*(4-l)
plt.plot(l,V(l))
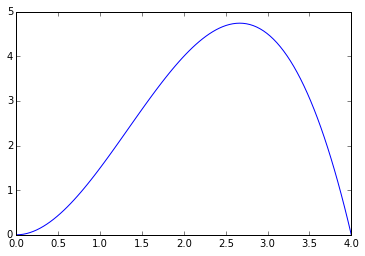
通过观察函数图,不难看出,在的值大约在
往上去一点的位置处,获得的纸盒的体积最大。
关键点(Critical Points)
通过导数一节,我们知道一个函数在某处的导数所描述的是:当输入值在该位置附近变化时,函数值所发生的相应变化。
因此,如果给定一个函数,如果知道在点
处函数的导数不为
,则在该点出稍微改变函数的输入值,函数值都会变化,这表示函数在该点的函数值即不可能是局部最大值,也不可能是局部最小值。相反,如果函数
在点
处函数的导数为
,或者该点出的导数不存在则称这个点就被称为关键点。
要想知道一个的关键点处,函数值
是一个局部最大值还是局部最小值,可以使用二次导数测试:
- 如果
,则函数
在
处的函数值是局部最小值
- 如果
,则函数
在
处的函数值是局部最大值
- 如果
,则测试无法告诉我们结论
二次导数测试在中学书本中,大多是要求不求甚解地记忆的规则,其实理解起来非常容易。二次导数测试中涉及到函数在某一点处的函数值、一次导数和二次导数,于是想在
处的泰勒级数:
因为为关键点,
,因而:
表明时,函数
在
附近的表现近似于二次函数,二次项的系数
决定了抛物线的开口朝向,因而决定了函数值在该点是怎样的。
回到之前的求最大盒子体积的优化问题,解法如下:
from sympy.abc import l
V = 0.5*l**2*(4-l)
# 看看一次导函数:
print V.diff(l)
# output is : -0.5*l**2 + 1.0*l*(-l + 4)
# 一次导函数的定义域为(-oo,oo),因此关键点为V'(l)=0的根
cp = sympy.solve(V.diff(l),l)
print cp
# output is: [0.0, 2.66666666666667]
# 找到关键点后,使用二次导数测试:
for p in cp:
print V.diff(l,2).subs(l,p)
# output is: 4, -4
# 因此知道在l=2.666666处时,纸盒的体积最大
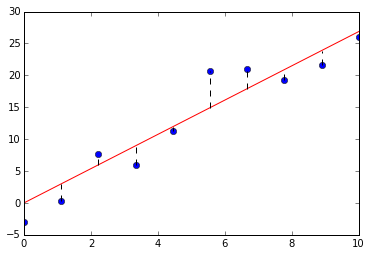
线性回归(Linear Regression)
二维平面上有个数据点,
,现尝试找到一条经过原点的直线
,使得所有数据点到该直线的残差(数据点和回归直线之间的水平距离)的平方和最小。
# 设定好随机函数种子,确保模拟数据的可重现性
np.random.seed(123)
# 随机生成一些带误差的数据
x = np.linspace(0,10,10)
res = np.random.randint(-5,5,10)
y = 3*x + res
# 求解回归线的系数
a = sum(x*y)/sum(x**2)
# 绘图
plt.plot(x,y,'o')
plt.plot(x,a*x,'red')
for i in range(len(x)):
plt.axvline(x[i],min((a*x[i]+5)/35.0,(y[i]+5)/35.0),\
max((a*x[i]+5)/35.0,(y[i]+5)/35.0),linestyle = '--',\
color = 'black')
要找到这样一条直线,实际上是一个优化问题:
要找出函数的最小值,首先计算一次导函数:
令该函数为,求解出关键点:
使用二次导数测试:
因此是能够使得函数值最小的输入。
这也是上面Python代码中,求解回归线斜率所用的计算方式。
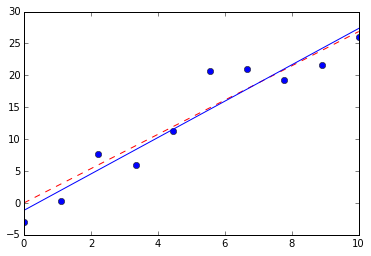
如果我们不限定直线一定经过原点,即公式为,则同样还是一个优化问题,只不过涉及的变量变成2个而已:
这个问题就是多元微积分里所要分析的问题了。
虽然在第二部分才会介绍具体解法,这里先给出一种Python中的求解方法:
slope, intercept = np.polyfit(x,y,1)
plt.plot(x,y,'o')
plt.plot(x,a*x,'red', linestyle = '--')
plt.plot(x,slope*x+intercept, 'blue')