极限

极限(Limits)

函数的极限，描述的是输入值在接近一个特定值时函数的表现。

定义：我们若要称函数在处的极限为即：，则需要：
对任意一个，我们要都能找到一个使得当的取值满足时

本节的重点内容其实是用Python画图...：

    f = lambda x: x**2-2*x-6
    x = np.linspace(0,5,100)
    y = f(x)

    plt.plot(x,y,'red')
    plt.grid('off')

    l = plt.axhline(-8,0,1,linewidth = 2, color = 'black')
    l = plt.axvline(0,0,1,linewidth = 2, color = 'black')

    l = plt.axhline(y=2,xmin=0,xmax=0.8,linestyle="--")
    l = plt.axvline(x=4,ymin=0,ymax=float(5)/9, linestyle = "--")

    l = plt.axhline(-6,3.7/5,4.3/5,linewidth = 2, color = 'black')
    l = plt.axvline(1,6.0/18,14.0/18,linewidth = 2, color = 'black')

    p = plt.axhspan(-2,6,0,(1+sqrt(13))/5,alpha = 0.15, ec = 'none')
    p = plt.axvspan((1+sqrt(5)),(1+sqrt(13)),0,1.0/3,alpha = 0.15, ec = 'none')

    p = plt.axhspan(f(3.7),f(4.3),0,4.3/5,alpha = 0.3, ec = 'none')
    p = plt.axvspan(3.7,4.3,0,(f(3.7)+8)/18,alpha = 0.3, ec = 'none')

    plt.axis([0,5,-8,10])


    plt.text(0.8,-1,r"$\epsilon$", fontsize = 18)
    plt.text(0.8,4,r"$\epsilon$", fontsize = 18)
    plt.text(3.75,-7.0,r"$\delta$", fontsize = 18)
    plt.text(4.1,-7.0,r"$\delta$", fontsize = 18)
    plt.text(3.95,-7.8,r"$a$", fontsize = 18)
    plt.text(4.5,8.5,r"$f(x)$", fontsize = 18,color="red")


    plt.show()

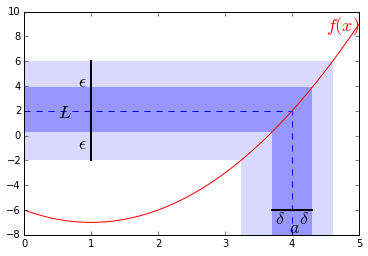
下面尝试用上面的定义来证明:
依据定义，我们需要show的是：对于任意,能找到一个使得：时有
注意到，其中我们已经知道
依三角不等式有：
因此
现在我们只需要找到一个满足即可
动用一些中学时候的二元一次方程知识应该很容易证明这样的是存在的，或者我们只要令即可使得且，因而

Python中求该极限方法如下：

    x = sympy.Symbol('x',real = True)
    y = f(x)
    print y.limit(x, 2)
    # result is: 2

上图中的函数就是,并且

至于趋近于的极限定义，就留给读者自己回忆啦。

函数的连续性

极限可以用来判断一个函数是否为连续函数。
当极限存在，且时，称函数在点处为连续的。 当一个函数在其定义域中任何一点处均连续，则称该函数是连续函数。

泰勒级数用于极限计算

我们在中学课本中一定记忆了常见的极限，以及极限计算的规则，这里我们便不再赘言。泰勒级数也可以用于计算一些形式比较复杂的函数的极限。这里，仅举一例：

洛必达法则（l'Hopital's rule）

利用泰勒级数来计算极限，有时也会陷入困境，例如：求极限的位置是在我们不知道泰勒展开的位置，或者所求极限是无穷的。通常遇到这些情况我们会使用各种形式的洛必达法则，读者可以自行回顾一下这些情形，这里我们仅尝试说明形式的洛必达法则为何成立。
如果和是连续函数，且。若 存在，则：

若分子分母同时求导后仍然是形式，那么便重复该过程，直至问题解决。 运用泰勒级数，我们很容易可以理解洛必达法则为什么会成立:




感兴趣的读者可以自己尝试去验证一下其他形式的洛必达法则。