泰勒级数

泰勒级数(Taylor Series)

在前几章的预热之后，读者可能会有这样的疑问，是否任何函数都可以写成友善的多项式形式呢？目前为止，我们介绍的都有其奇妙的多项式形式。这些多项式形式实际为这些函数在处展开的泰勒级数。

下面我们给出函数在处展开的泰勒级数的定义：

其中：表示函数的次导函数在点处的取值。

我们知道对无论计算多少次导数结果都是（前面也推荐读者自己验证过），即：

因而，依据上面的定义展开有：
便得到了在1.1中所介绍的公式。

类似地，有兴趣的读者可以尝试用泰勒级数的定义来推导一下关于处展开的泰勒级数。

多项式近似(Polynomial Approximantion)

泰勒级数可以把非常复杂的函数转变成无限项的和的形式。通常，我们可以只计算泰勒级数的前几项之和，便能够获得原函数的局部近似了。在做这样的多项式近似时，我们所计算的项越多，则近似的结果越精确。

下面，在Python中试试吧：

    import sympy 
    # 指定x为符号
    x = sympy.Symbol('x')
    # exp为公式
    exp = e**x
    # 下面开始求和,就求前21项的和吧
    sums = 0
    for i in range(20):
        # 求i次导函数
        numerator = exp.diff(x,i)
        # 计算导函数在x=0处的值
        numerator = numerator.evalf(subs={x:0})
        denominator = np.math.factorial(i)
        sums += numerator/denominator*x**i

    # 下面检验一下原始的exp函数和其在x=0处展开的泰勒级数前20项之和的差距
    print exp.evalf(subs={x:0})-sums.evalf(subs={x:0})
    # result is 0
    xvals = np.linspace(0,20,100)

    for xval in xvals:
        plt.plot(xval,exp.evalf(subs={x:xval}),'bo',\
                 xval,sums.evalf(subs={x:xval}),'ro')

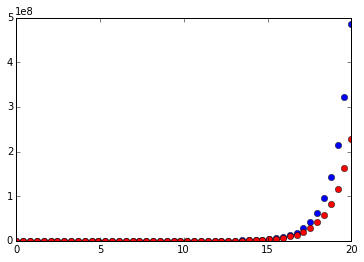
表明指数函数在处展开的泰勒级数只取前20项的话，在输入值越接近展开点（）处的近似效果就越好。

让我们看看采用不同项数所计算出来的近似结果之间的差异：

    def polyApprox(func,num_terms):
        # 当我们需要反复做类似的步骤的时候，最好将步骤定义为一个函数
        sums = 0
        for i in range(num_terms):
            numerator = func.diff(x,i)
            numerator = numerator.evalf(subs={x:0})
            denominator = np.math.factorial(i)
            sums += numerator/denominator*x**i
        return sums

    sum5 = polyApprox(exp,5)
    sum10 = polyApprox(exp,10)

    # 利用sympy我们也可以获得泰勒级数：
    sum15 = exp.series(x,0,15).removeO()

    xvals = np.linspace(5,10,100)
    for xval in xvals:
        plt.plot(xval,exp.evalf(subs={x:xval}),'bo',\
                 xval,sum5.evalf(subs={x:xval}),'ro',\
                 xval,sum10.evalf(subs={x:xval}),'go',\
                 xval,sum15.evalf(subs={x:xval}),'yo')

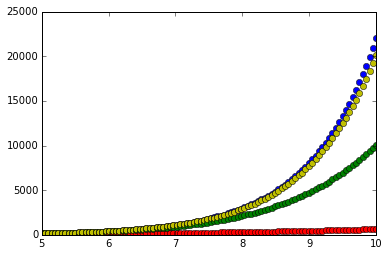
可以明显看出，在输入值远离展开点处时，用越多项数获得的近似结果越接近真实值。

展开点（Expansion point）

上面我们获得的泰勒级数都是围绕着处获得的，我们发现多项式近似也只在处较为准确。如果我们希望在其他位置获得类似的多项式近似，则可以在不同的展开点（例如）获得泰勒级数：

Python中，这也非常容易：

    def taylorExpansion(func,var,expPoint,numTerms):
        return func.series(var,expPoint,numTerms)

    print taylorExpansion(sympy.tanh(x),x,2,3)
    # resulut is :tanh(2) + (x - 2)*(-tanh(2)**2 + 1) + (x - 2)**2*(-tanh(2)\
        + tanh(2)**3) + O((x - 2)**3, (x, 2))