牛顿迭代法

求二次根

各位同学可能遇到过这样的编程题目，要求在不使用或的前提下，求解的正二次根。
可以用牛顿迭代法解：

    def mysqrt(c, x = 1, maxiter = 10, prt_step = False):
        for i in range(maxiter):
            x = 0.5*(x+ c/x)
            if prt_step == True:
                # 在输出时，{0}和{1}将被i+1和x所替代
                print "After {0} iteration, the root value is updated to {1}".format(i+1,x)
        return x

    print mysqrt(2,maxiter =4,prt_step = True)
    # After 1 iteration, the root value is updated to 1.5
    # After 2 iteration, the root value is updated to 1.41666666667
    # After 3 iteration, the root value is updated to 1.41421568627
    # After 4 iteration, the root value is updated to 1.41421356237
    # result : 1.4142135623746899

牛顿迭代法（Newton's Itervative Method）

上面的求正二次根问题，等价于求的正根 根据上一节介绍的线性近似：
如果是的一个根，即，则：

因此，如果我们对的正根有一个初始估计，便可以用上面的近似不断获取更加准确的估计值，方法为：

将带入上式，便会得到代码中的跟新规则了。

通过绘图我们能进一步了解这个方法（喜闻乐见的绘图时刻又到了！）：

    f = lambda x: x**2-2*x-4
    l1 = lambda x: 2*x-8
    l2 = lambda x: 6*x-20

    x = np.linspace(0,5,100)

    plt.plot(x,f(x),'black')
    plt.plot(x[30:80],l1(x[30:80]),'blue', linestyle = '--')
    plt.plot(x[66:],l2(x[66:]),'blue', linestyle = '--')

    l = plt.axhline(y=0,xmin=0,xmax=1,color = 'black')
    l = plt.axvline(x=2,ymin=2.0/18,ymax=6.0/18, linestyle = '--')
    l = plt.axvline(x=4,ymin=6.0/18,ymax=10.0/18, linestyle = '--')

    plt.text(1.9,0.5,r"$x_0$", fontsize = 18)
    plt.text(3.9,-1.5,r"$x_1$", fontsize = 18)
    plt.text(3.1,1.3,r"$x_2$", fontsize = 18)


    plt.plot(2,0,marker = 'o', color = 'r' )
    plt.plot(2,-4,marker = 'o', color = 'r' )
    plt.plot(4,0,marker = 'o', color = 'r' )
    plt.plot(4,4,marker = 'o', color = 'r' )
    plt.plot(10.0/3,0,marker = 'o', color = 'r' )

    plt.show()

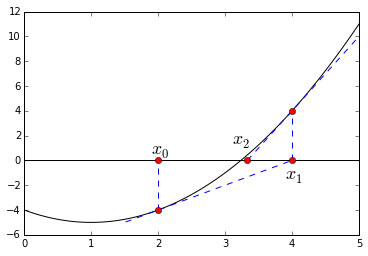
我们要猜的解，从的初始猜测值开始，找到在处的切线，找到其与的交点，将该交点更新为新的猜测的解，如此循环。

如下定义牛顿迭代法：

    def NewTon(f, s = 1, maxiter = 100, prt_step = False):
        for i in range(maxiter):
            # 相较于f.evalf(subs={x:s}),subs()是更好的将值带入并计算的方法。
            s = s - f.subs(x,s)/f.diff().subs(x,s)
            if prt_step == True:
                print "After {0} iteration, the solution is updated to {1}".format(i+1,s)
        return s

    from sympy.abc import x
    f = x**2-2*x-4
    print NewTon(f, s = 2, maxiter = 4, prt_step = True)
    # After 1 iteration, the solution is updated to 4
    # After 2 iteration, the solution is updated to 10/3
    # After 3 iteration, the solution is updated to 68/21
    # After 4 iteration, the solution is updated to 3194/987
    # 3194/987

Sympy可以帮助我们求解方程，不要教坏小朋友们哦：

    sympy.solve(f,x)
    # result: [1 + sqrt(5), -sqrt(5) + 1]