通过微分方程建模
1 数学建模(Mathematical Modeling)
数学建模是用数学公式来描述现实世界中现象的过程,其主要任务是识别关键数量以及发现这些数量之间的数学关系,通常通过如下三步实现:
- 提出前提假设(assumption)
- 识别相关的变量和参数
- 根据1中前提假设对2中的变量构建数学公式
数学模型中的数量可以分为三种:
- 自变量(independent variable)
- 因变量或简称变量(dependent variable)
- 参数(parameter)
用微分方程来构建的数学模型的前提假设中通常会包含导数,其文字表述通常会包含“增长率(rate of increase)”、“变化率(rate of change)”、“速度(velocity)”、“加速度(acceleration)”一类词语。
例:跳伞
- 前提假设:跳伞者只收到重力和摩擦力影响,摩擦力与速度的平方成正比,以及牛顿第二定律:$$F=ma$$。
- 变量:
- 自变量:t 时间(秒)
- 因变量:v 速度
- 参数:
- g 重力常数
- m 跳伞者的质量
- k 阻力的系数
- 建模:
- 等式左边,跳伞者收到的力:$$F=mg-kv^2$$
- 等式右边:$$m\frac{dv}{dt}$$
- 模型为:$$mg-kv^2=m\frac{dv}{dt}$$
得到的模型:$$mg-kv^2=m\frac{dv}{dt}$$是一阶常微分方程(first order ordinary differential equation),其解法是去寻找一个满足方程的函数$$v(t)$$。
2 建模人口增长
用微分方程建模美国人口增长。
# libararies
import numpy as np
import matplotlib.pyplot as plt
# the data
USPop = np.array([3.9,5.3,7.2,9.6,12.9,
17.1,23.2,31.4,38.6,50.2,
63.0,76.3,92.0,105.7,122.8,
131.7,151.3,179.3,203.3,226.5,
248.7,281.4,308.7])
Year = np.array(range(1790,2011,10))
# plotting the data as scatter plot
plt.plot(Year,USPop,'bo')
plt.title("U.S. Census 1790-2010")
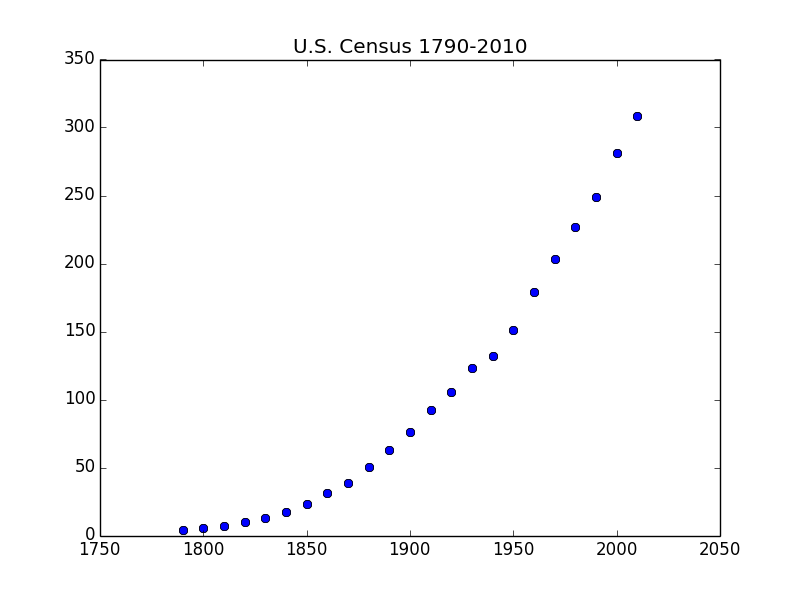
先看一个最简单的模型:马尔萨斯增长模型(Malthusian Growth Model)
- 前提假设: 人口的增长速率与人口数量成正比
- 变量:
- 自变量: t 时间(年,从1790年开始)
- 因变量:p 人口 (百万)
- 参数:
- k 人口的增长速率与人口数量所成的比率
- 模型:
- 等式左边,人口的增长率:$$\frac{dp}{dt}$$
- 等式右边:$$kp$$
- 模型为:$$\frac{dp}{dt}=kp$$
在获得模型后,我们的目标是:找到一个满足公式的函数$$p(t)$$
方法一分析方法(Analytic Method):
$$\frac{dp}{dt}=kp\ \frac{1}{p}\frac{dp}{dt}=k\ \int\frac{1}{p}\frac{dp}{dt}dt=\int{k}dt\ \int\frac{1}{p}dp=kt+C\ \ln(p)=kt+C\ p=e^{kt+C}\ p=e^{kt}e^C\ p=Ke^{kt}\ p(t)=Ke^{kt}
$$
若我们通过$$1790$$年和$$1800$$年的数据来拟合模型,则:
$$p(0)=K=3.9$$
$$p(10)=3.9e^{10k}=5.3\implies k = 0.03067$$
因此模型为:$$p(t)=3.9e^{0.03067t}$$
绘图看一下模型的好坏:
# library
import sympy
from sympy.abc import t
from sympy import E as e
# model
p = 3.9*e**(0.03067*t)
# domain
domain = np.array(range(0,len(USPop)*10,10))
# plot actual data and model prediction
plt.plot(Year,USPop,'bo')
plt.plot(Year,[p.subs(t,year) for year in domain])
# limit the y axis to see the lower part of the graph
plt.axis(ymax = 300)

看到1850年前,模型的预测与真实值还是较为吻合的,之后出现较大偏差。
3 有限资源与罗吉斯特人口模型
因为自然资源是有限的,因此人口的增长会受到限制,因此对上面的模型进行如下修改:
- 人口数量较少时,人口的增长速率与人口数量成正比
- 随着人口的增长,人口的相对增长率(relative growth rate)逐渐减小
人口的相对增长率定义为:
$$\text{relative growth rate} = \frac{(\frac{dp}{dt})}{p}=\frac{1}{p}\frac{dp}{dt}$$
罗吉斯特人口模型:
- 前提假设:人口的增长率与人口数量呈反比,即人口的相对增长率与人口数量成反比
- 变量:
- 自变量: t 时间(年,从1790年开始)
- 因变量:p 人口 (百万)
- 参数:
- k
- m 人口增长速度随人口数量变化而变化的比率
- 模型:
- 等式左边,人口的相对增长率:$$\frac{1}{p}\frac{dp}{dt}$$
- 等式右边:$$k+mp$$
- 模型为:$$\frac{1}{p}\frac{dp}{dt}=k+mp$$
方法二数值方法(Numerical Method)
模型$$\frac{1}{p}\frac{dp}{dt}=k+mp$$是一条直线,需要拟合的是参数k和m,看一下手头的数据:
| t | p |
|---|---|
| 0 | 3.9 |
| 10 | 5.3 |
| 20 | 7.2 |
从导数的切线解读出发,可以做如下估计:
$$\frac{dp}{dt}\bigg|{t=10}\approx\frac{p(20)-p(0)}{20}= 0.165 $$
因此相对增长率$$\frac{1}{p}\frac{dp}{dt}\bigg|{t=10}=\frac{1}{5.2}\times 0.165=0.03173076923076923$$
类似地,可以计算各个时刻的相对增长率,画图后可以发现,相对增长率大致可以用直线来拟合,拟合一条回归线。
# calculate relative growth rate
rgr = [1.0/USPop[i]*(USPop[i+1]-USPop[i-1])/20 for i in range(1,len(USPop)-1)]
# fit a line to the data
slope, intercept = np.polyfit(USPop[1:-1],rgr,1)
print slope, intercept
# result is: -8.2111607647e-05 0.0280801486169
# make a plot
plt.plot(USPop[1:-1],rgr,'bo')
plt.plot(np.array(range(0,350)),slope*np.array(range(0,350))+intercept)
plt.text(344,0.001,'N',fontsize = 18,color="black")
plt.axis(ymin = 0)
plt.axis(xmax = 400)
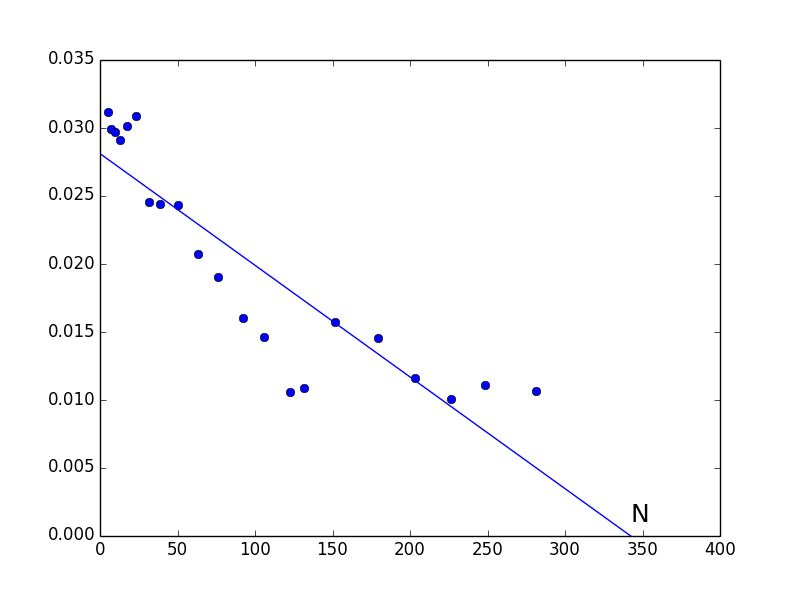
得到人口的相对增长率函数为:$$\frac{1}{p}\frac{dp}{dt}=0.02808 + 0.000082111\times p$$
因此得到罗吉斯特微分方程:$$\frac{dp}{dt}=0.02808p+0.000082111\times p^2$$
该微分方程的分析解法留给后面介绍,先用欧拉方法试一试该微分方程的近似效果如何:
# euler's method
from sympy.abc import p
pred = [3.9]
logistModel = intercept*p+slope*p**2
# step is 10
for i in range(22):
pred.append(logistModel.subs(p,pred[-1])*10+pred[-1])
# make a plot
plt.plot(Year,USPop,'bo',Year,pred)
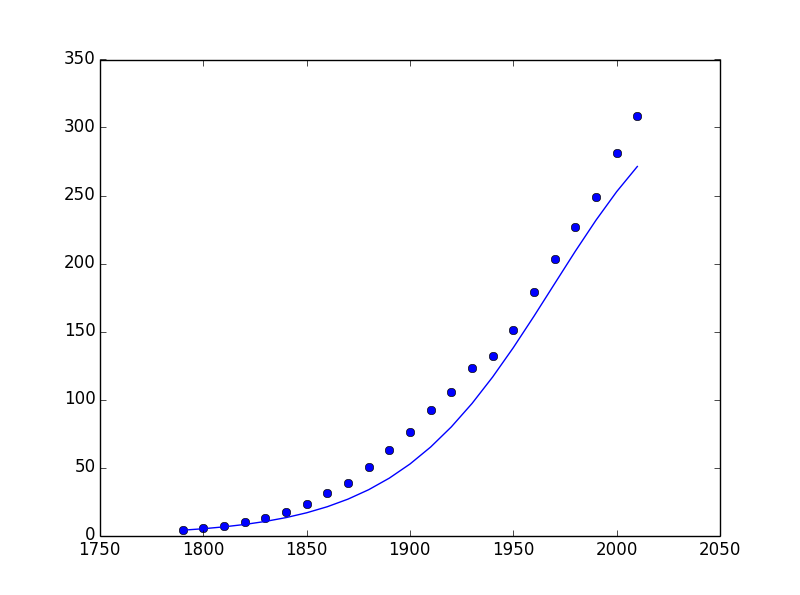
发现近似效果比之前的马尔萨斯增长模型要更加好。
4 定性分析(Qualitative analysis)
3中得到人口的相对增长率,$$\frac{1}{p}\frac{dp}{dt}=k+mp$$,从函数图上看,回归线$$k+mp$$交$$p$$轴于点$$N$$。
- 在人口$$p<N$$时,增长率是正的,表示人口将增加
- 在人口$$p>N$$时,增长率是负的,表示人口将减少
用$$N$$和$$p$$表示$$m$$并带入罗吉斯特模型获得:
$$\frac{1}{p}\frac{dp}{dt}=k-\frac{k}{N}p$$
简单变换得到罗吉斯特微分方程:
$$\frac{dp}{dt}=kp-\frac{k}{N}p^2$$
注意到这是一个关于$$p$$的二次函数,二次项前系数为负,即开口朝下:
pdomain = np.array(range(-20,380,10))
plt.plot(pdomain, [logistModel.subs(p,pval) for pval in pdomain])
plt.axhline(0,0,1,linewidth = 2, color = 'black')
plt.axvline(0,0,1,linewidth = 2, color = 'black')
plt.text(342,0.001,'N',fontsize = 18,color="black")
plt.text(-20,2,r'$\frac{dp}{dt}$',fontsize = 18,color="black")
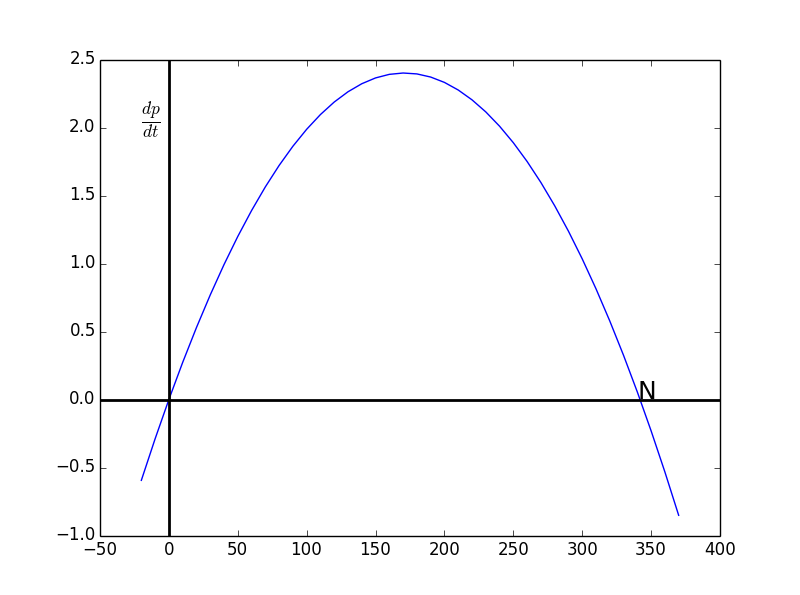
从定性的角度去分析人口随时间的变化:
- $$p(0)=0\implies \forall t >0, p(t) = 0$$
- $$p(0)=N\implies \forall t >0, p(t) = N$$
- $$0 < p(0) <N \implies \lim_{t\rightarrow \infty}p(t) = N$$
- $$p(0)>N \implies \lim_{t\rightarrow \infty}p(t) = N$$
因此,$$N$$也被称为承载能力(carrying capacity)