斜率场
斜率场(slope field)
微分方程$$\frac{dy}{dt}=f(t,y(t))$$的右边:$$f(t,y(t))$$定义了一个斜率场,即在$$t-y$$平面上的一张可以用来描述该微分方程的图。
取$$t-y$$平面上的任意一点$$(t_i,y_i)$$,则$$f(t_i,y_i)$$表示的是经过该点的微分方程解在该点处切线的斜率。
例如之前章节中涉及的微分方程:$$\frac{dy}{dt}=-2ty^2$$
知道其解形式为:$$y(t) = \frac{1}{t^2+C}$$
若给定初值$$y(0)=2$$,其解为:$$y(t)=\frac{1}{t^2+\frac{1}{2}}$$
下面列举该解所经过的几个点,以及相应位置切线的斜率:
| $$(t,y)$$ | $$ f(t,y)$$ | $$ y'(t) $$ |
|---|---|---|
| $$(0,2)$$ | 0 | 0 |
| $$(-1,\frac{2}{3})$$ | $$\frac{8}{9}$$ | $$\frac{8}{9}$$ |
| $$(1,\frac{2}{3})$$ | $$\frac{8}{9}$$ | $$\frac{8}{9}$$ |
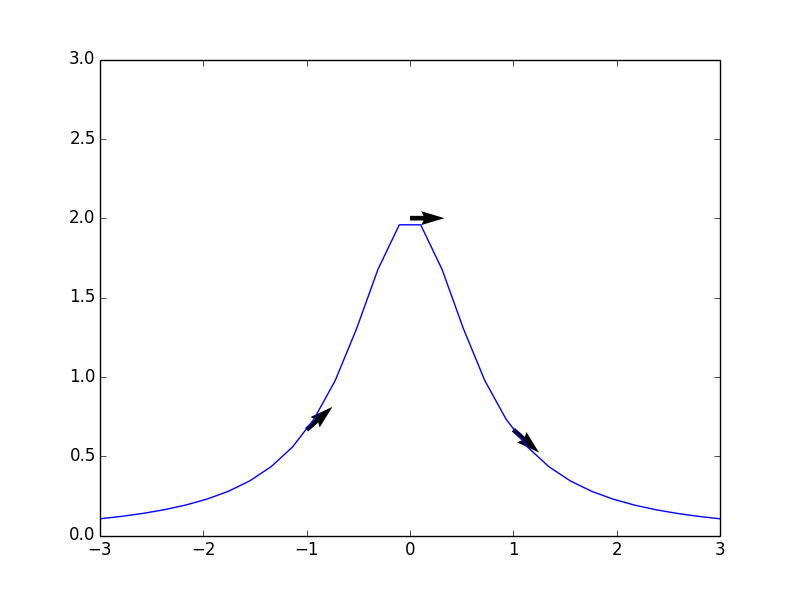
绘图表示为:
# library
import matplotlib.pyplot as plt
from sympy.abc import t
import numpy as np
# define the function
y = 1.0/(t**2+1.0/2)
# sample domain
domain = np.linspace(-3,3,30)
# calculate 3 slopes at tabled position
T = np.array([-1,0,1])
Y = np.array([2.0/3,2,2.0/3])
U = 2
V = -2*T*Y**2
N = np.sqrt(U**2+V**2)
U2, V2 = U/N, V/N
# make the plot
plt.plot(domain, [y.subs(t, tval) for tval in domain])
plt.quiver( T,Y,U2, V2)
plt.xlim([-3,3])
plt.ylim([0,3])
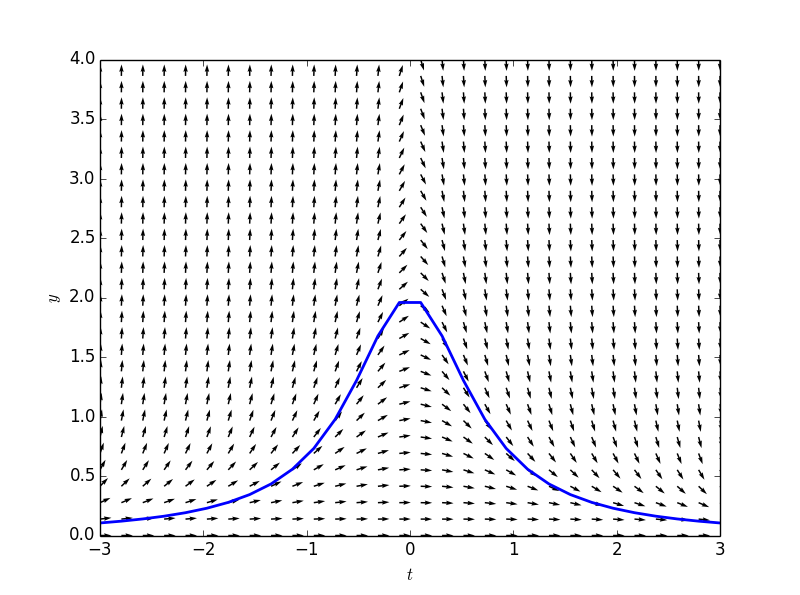
下面是微分方程的斜率场,箭头代表的含义是:取$$t-y$$平面上的一个点,找到经过该点的微分方程的解(函数y(t)),求出该函数在该点处切线的方向,将该方向用箭头表示。
import matplotlib.pyplot as plt
from sympy.abc import t
import numpy as np
f = 1.0/(t**2+1.0/2)
domain = np.linspace(-3,3,30)
T,Y = np.meshgrid(domain,np.linspace(0,4,30) )
U = 1
V = -2*T*Y**2
N = np.sqrt(U**2+V**2)
U2, V2 = U/N, V/N
fig = plt.figure(num=1)
ax=fig.add_subplot(111)
ax.quiver( T,Y,U2, V2)
plt.plot(domain,np.array([f.subs(t, tval) for tval in domain]), linewidth= 2)
plt.xlim([-3,3])
plt.ylim([0,4])
plt.xlabel(r"$x$")
plt.ylabel(r"$y$")
plt.show()
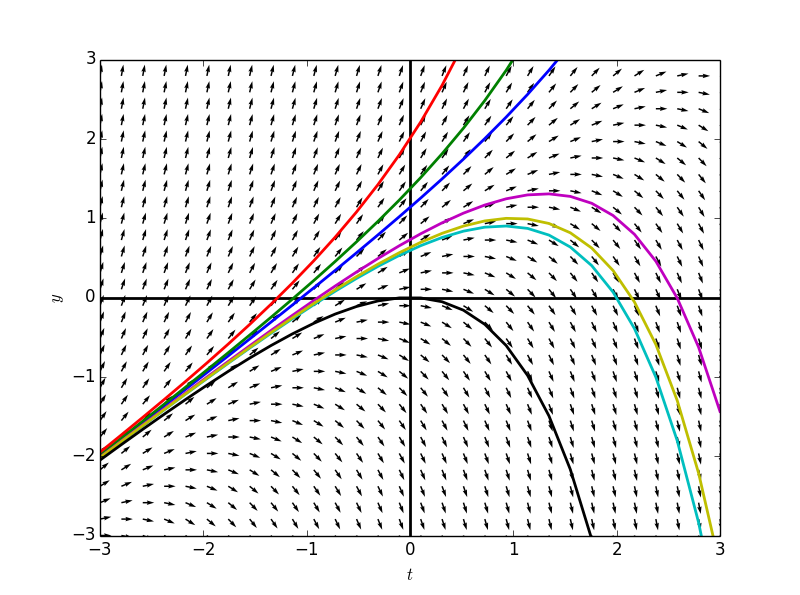
在斜率场图中,任选一点,可以不断沿着斜率方向向前、向后绘制出函数图,而该函数图即为经过所选点的微分方程的解。
下面绘制出微分方程$$\frac{dy}{dt}=y-t$$的斜率场,并且选中若干点:$$(2,4),(1,3),(0,2),(2,0),(2,1),(1,1),(0,0)$$,分别绘制出相应的解的函数图。
def plotSlopeField(tdomain,ydomain,formula,points = []):
# initialize figure
fig = plt.figure(num=1)
# create grid
T,Y = np.meshgrid(tdomain,ydomain )
# calculate slope vectors
U = 1
V = np.array([[formula.subs({y(t): yval, t: tval}) for tval in tdomain] for yval in ydomain],dtype = 'float')
N = np.sqrt(U**2+V**2)
U2, V2 = U/N, V/N
# make the plot
plt.quiver( T,Y,U2, V2)
plt.xlabel(r"$t$")
plt.ylabel(r"$y$")
plt.axhline(0,0,1,linewidth = 2, color = 'black')
plt.axvline(0,0,1,linewidth = 2, color = 'black')
# solve the differential equation
from sympy import Derivative, dsolve
try:
solutions = dsolve(Derivative(y(t),t)-formula,y(t)).args[1]
except:
solutions = 0
# plot the solutions through the given points
if points != []:
for p in points:
from sympy import Eq, solve
C1 = solve(Eq(solutions.subs(t,p[0]),p[1]))[0]
solution = solutions.subs('C1',C1)
plt.plot(tdomain, np.array([solution.subs(t,tval) for tval in tdomain],dtype= 'float'),
linewidth = '2')
# limiting the axes
plt.xlim([tdomain[0],tdomain[-1]])
plt.ylim([ydomain[0],ydomain[-1]])
return fig
domain = np.linspace(-3,3,30)
from sympy.abc import t
from sympy import Function
y = Function('y')
formula = y(t) - t
fg = plotSlopeField(domain,domain,formula,[(2,4),(1,3),(0,2),(2,0),(2,1),(1,1),(0,0)])
fg.show()
exercise:
绘制$$y'=y/2 + (.2)(t-1)^2$$的斜率场,找到经过$$(5,5)$$的解。
formula2 = 0.2*(t - 1)**2 + 0.5*y(t)
domain2 = np.linspace(-5,5,30)
fg2 = plotSlopeField(domain2,domain2,formula2,[(5,5)])
fg2.show()

特例1
两个值得我们特别注意的特例:
$$\frac{dy}{dt}=f(t)$$
即右边只包含$$t$$,若给定一个$$t$$值$$t_0$$,则经过该点垂直于$$t$$轴的直线$$t=t_0$$上的任意一点在斜率场中的方向均相同(平行)。
任意一个解都可以视为是将另一个解沿着竖直方向移动获得的。
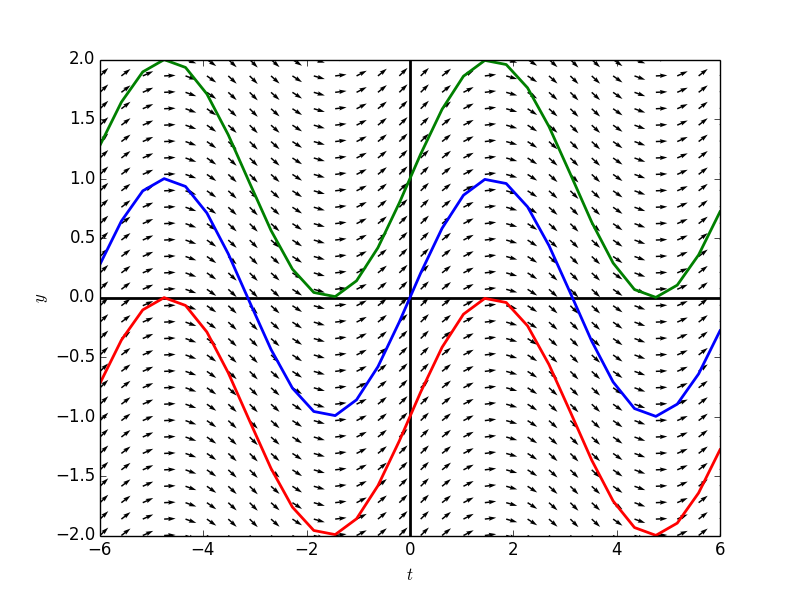
例如:$$\frac{dy}{dt}=cost$$
一般解为:$$y(t)=(sint)+C$$
其中$$C$$是任意常数,不同的解之间只有常数项不同,相当于将$$sint$$的函数图,沿着竖直方向移动获得的。
import sympy
formula3 = sympy.cos(t)
tdomain3 = np.linspace(-6,6,30)
ydomain3 = np.linspace(-2,2,30)
fg3 = plotSlopeField(tdomain3,ydomain3,formula3,[(0,0),(0,1),(0,-1)])
fg3.show()
练习:
Use dfield to plot the slope field for $$\frac{dy}{dt}=t(t^2−1)$$ on a window with −2≤t≤2 and −1≤y≤1.
formula4 = t*(t**2-1)
tdomain4 = np.linspace(-2,2,30)
ydomain4 = np.linspace(-1,1,30)
fg4 = plotSlopeField(tdomain4,ydomain4,formula4)
fg4.show()

特例2
另一个特例是:
$$\frac{dy}{dt}=f(y)$$
这样的斜率场是沿着水平直线上的各点的斜率方向均平行的。
任意一个解都可以视为是将另一个解沿着水平方向移动获得的。
例如:
$$\frac{dy}{dt}=y(1-y)$$
其一般解为:
$$y(t)=\frac{e^t}{1+e^t}$$
formula5 = y(t)*(1-y(t))
tdomain5 = np.linspace(-8,8,30)
ydomain5 = np.linspace(-1,2,30)
fg5 = plotSlopeField(tdomain5,ydomain5,formula5,[(1,1),(1,0.5),(-2,0.5),(3,0.5)])
fg5.show()

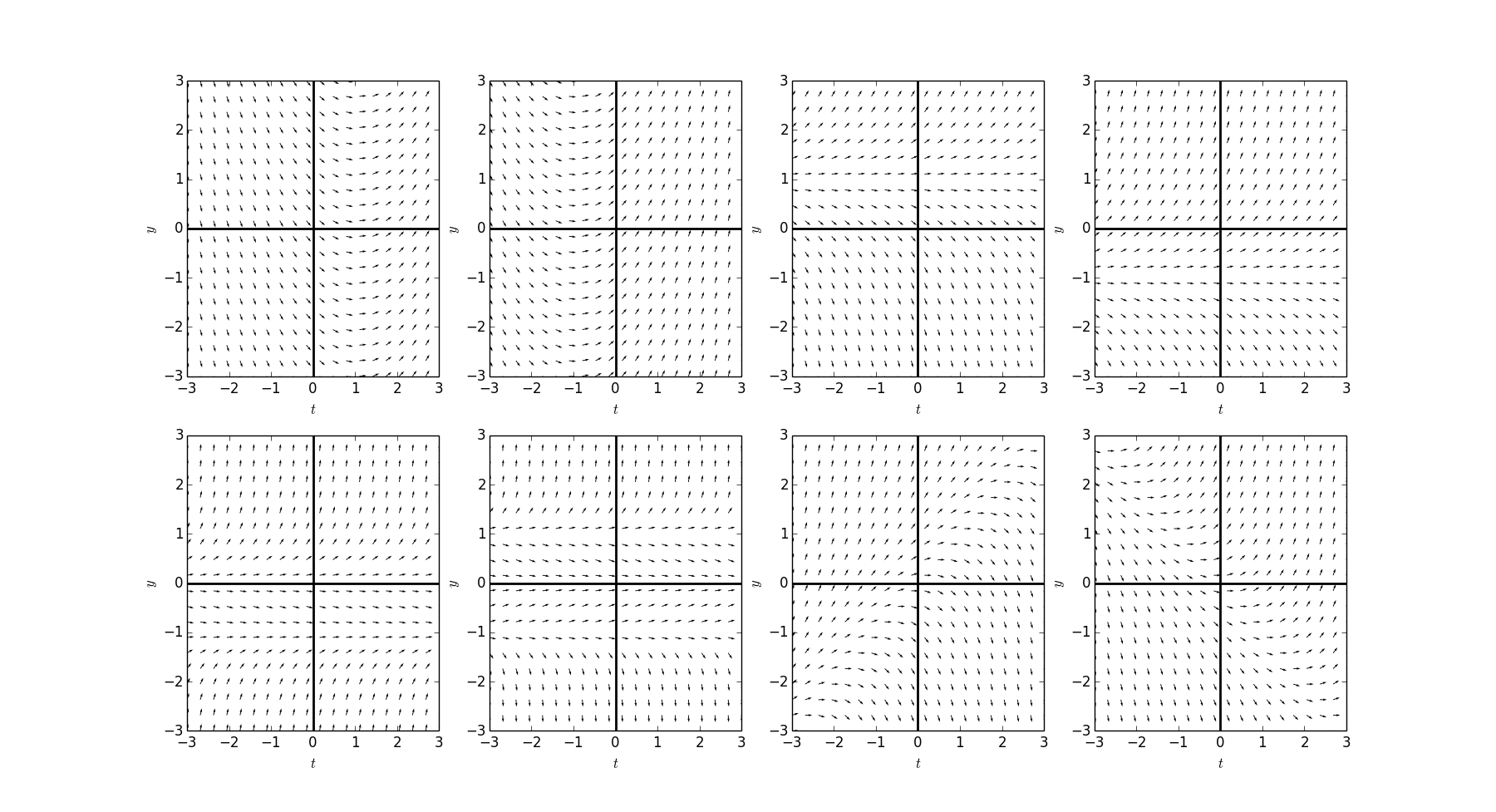
练习:
formulas = [t-1,
t+1,
y(t)+1,
y(t)-1,
y(t)**2+y(t),
y(t)*(y(t)**2-1),
y(t)-t,
y(t)+t]
tdomainm = np.linspace(-3,3,20)
ydomainm = np.linspace(-3,3,20)
for i in range(len(formulas)):
plt.subplot(2,4,i+1)
plotSlopeField(tdomainm,ydomainm,formulas[i],[])
plt.show()