微分方程组

弹簧-重物系统（Mass-Spring System）

假设有一个弹簧垂直挂在一个水平面下，现在给弹簧下方挂上一个重物。由牛顿第二定律有：
弹簧的拉力 = 挂着重物的质量 重物的加速度 $$F = ma = m \frac{d^2y}{dt^2}$$
又由胡可定律： 弹簧的拉力 = 系数 弹簧的位置变化 $$F = -ky$$

令两者相等有：

$$m\frac{d^2y}{dt^2} = -ky\ m\frac{d^2y}{dt^2} + ky = 0$$

这是一个二阶（二阶导数）自治（只有y没有t）微分方程

一般而言二阶自治微分方程包括：

1. 一个自变量
2. 一个因变量
3. 方程形式为：$$\frac{d^2y}{dt^2} = f(x, \frac{dy}{dt})$$

再有两个二阶自治方程的例子： 范德波尔方程（van der pol ）：

$$\frac{d^2x}{dt^2} - (1-x^2)\frac{dx}{dt} + x = 0$$ 达芬方程（duffing）：

$$\frac{d^2x}{dt^2} + b\frac{dx}{dt} + kx + x^3= 0$$

狐狸-兔子模型

开始进入一阶方程组的讨论。我们用最简单的捕猎（predator-prey）系统。假设捕食者是狐狸，猎物是兔子。

前提假设如下：

1. 如果没有狐狸，兔子的繁殖率与其当前数量成正比，并且没有上限
2. 如果没有兔子，狐狸的死亡率与其当前数量成正比
3. (兔子被狐狸吃掉的频率)与(狐狸与兔子相遇的频率)成正比
4. (狐狸繁殖率)与(兔子被捕杀的数量)成正比，即与(狐狸与兔子相遇的频率)成正比

变量：

• 自变量：时间 $$t$$
• 因变量：兔子的数量 $$R$$， 狐狸的数量 $$F$$

根据前提假设1,3：

$$\frac{dR}{dt} = aR - bRF$$
根据前提假设2,4：

$$\frac{dF}{dt} = - cF + dRF$$

两个方程一起，我们获得了方程组：

$$\frac{dR}{dt} = aR - bRF$$

$$\frac{dF}{dt} = - cF + dRF$$

其中参数$$a,b,c,d$$都是正数

上面的例子是一个一般一阶自治微分方程组，一般而言，一个一阶自治方程组包括：

1. 一个自变量
2. 两个因变量
3. 形式为:$$\begin{cases} \frac{dx}{dt} = f(x,y) \ \frac{dy}{dt} = g(x,y) \end{cases}$$

平衡解是两个函数$$R(t),F(t)$$使得方程组中两个方程永远成立。

$$\begin{cases} aR - bRF = R(a-bF) = 0 \ - cF + dRF = F(dR - c) = 0 \end{cases}$$
得出两个平衡解：

$$\begin{cases} R(t) = 0 \ F(t) = 0 \end{cases}$$ 以及：

$$\begin{cases} R(t) = \frac{c}{d} \ F(t) = \frac{a}{b} \end{cases}$$

回到我们的捕猎方程组，考虑一个具体问题，令参数如下：

$$a = 2, b = 1.2, c = 1, d = 0.9$$

$$\frac{dR}{dt} = 2R - 1.2RF$$

$$\frac{dF}{dt} = - F + 0.9RF$$ 不难发现有两组平衡解：$$(R(t),F(t) = (0,0)$$和$$(R(t),F(t))=(10/9,5/3)$$，若在$$R-F$$平面，称为相位平面(Phase Plane)，这两组解对应于两个点。

现在假设初值为:$$(R_0, F_0) = (1.0, 0.5)$$
用数值近似方法看一下$$R(t)$$和$$F(t)$$的表现：

    import numpy as np
    import sympy
    from sympy.abc import t
    from sympy import Function, Derivative, dsolve, Eq
    import matplotlib.pyplot as plt

    def reduceSize(Range, p):
        return [Range[i] for i in range(len(Range)) if i%p == 0]

    R = Function('R')
    F = Function('F')

    formulaR = 2*R(t) - 1.2*R(t)*F(t)
    formulaF = -1*F(t) + 0.9*R(t)*F(t)

    tdomain = np.array([i*0.0005 for i in range(32000)])
    dt = 0.0005
    Rrange = [1.0]
    Frange = [0.5]

    for t in tdomain[1:]:
    dR = formulaR.subs({'R(t)':Rrange[-1] , 'F(t)': Frange[-1]})
    dF = formulaF.subs({'R(t)':Rrange[-1] , 'F(t)': Frange[-1]})
    Rrange.append(Rrange[-1]+dt*dR)
    Frange.append(Frange[-1]+dt*dF)

    Trange = reduceSize(tdomain, 100)
    Rrange = reduceSize(Rrange, 100)
    Frange = reduceSize(Frange, 100)

    plt.plot(Trange,Rrange, 'lightblue',Trange,Frange, 'darkblue')

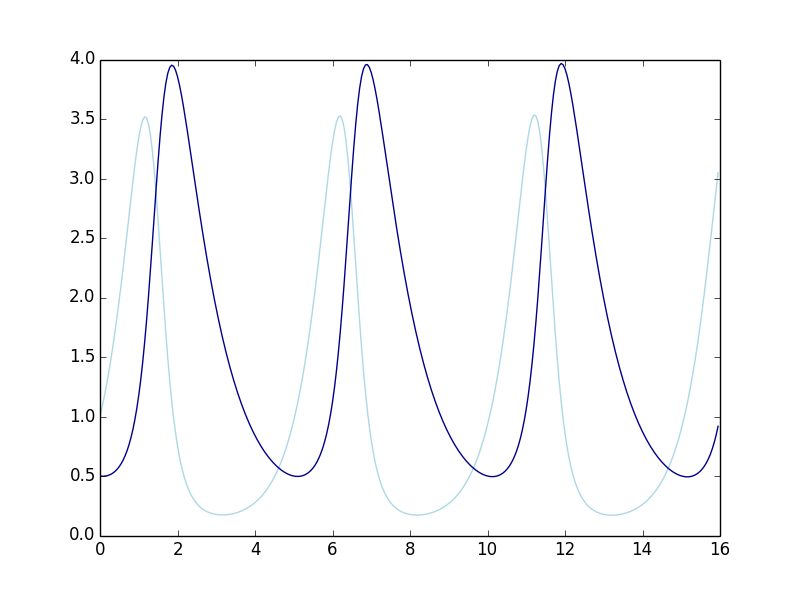兔子的数量是淡蓝色的曲线，狐狸的数量是深蓝色的曲线，发现两者都是在上下震荡着。上面这个图称为成分图（component graph）

看一看相位平面

    plt.plot(Rrange, Frange)

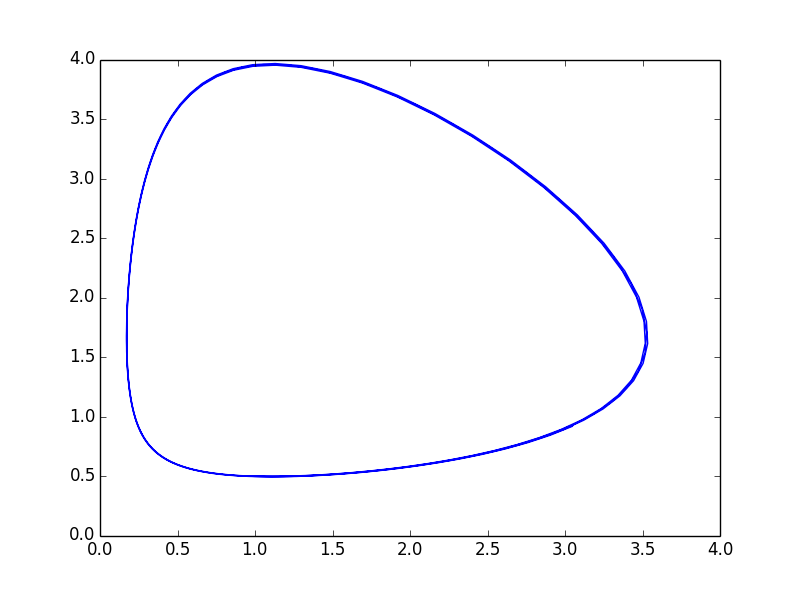横轴是兔子的数量，纵轴是狐狸的数量。在相位平面的这个曲线，被称为解曲线(solution curve)

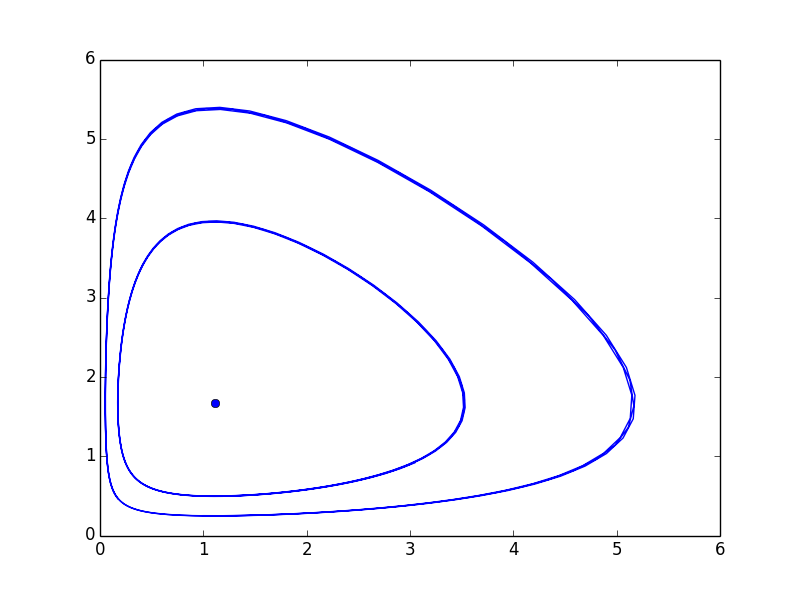
不同的初值，对应于相位平面内不同的解曲线，在同一个相位平面内，将方程组的多个解曲线绘制而出就成了相位图（phase portrait）

    Rrange2 = [1.0]
    Frange2 = [0.25]
    for t in tdomain[1:]:
        dR = formulaR.subs({'R(t)':Rrange2[-1] , 'F(t)': Frange2[-1]})
        dF = formulaF.subs({'R(t)':Rrange2[-1] , 'F(t)': Frange2[-1]})
        Rrange2.append(Rrange2[-1]+dt*dR)
        Frange2.append(Frange2[-1]+dt*dF)

    Rrange3 = [10.0/9]
    Frange3 = [5.0/3]

    plt.plot(Rrange, Frange, 'blue',
             Rrange2, Frange2, 'blue',
             Rrange3, Frange3, 'bo')

3D 交互图！ 拖动起来反应比较慢，比不上老师matlab里的图。

    fig = plt.figure()
    ax = fig.gca(projection='3d')
    ax.plot(Rrange, Frange, Trange)
    ax.plot(Rrange, Frange, [0 for t in Trange])
    ax.plot([0 for t in Trange], Frange, Trange)
    ax.plot(Rrange, [0 for t in Trange], Trange)
    ax.set_xlabel(r'$R(t)$')
    ax.set_ylabel(r'$F(t)$')
    ax.set_zlabel(r'$t$')
    plt.show()

从上往下看$$R-F$$平面

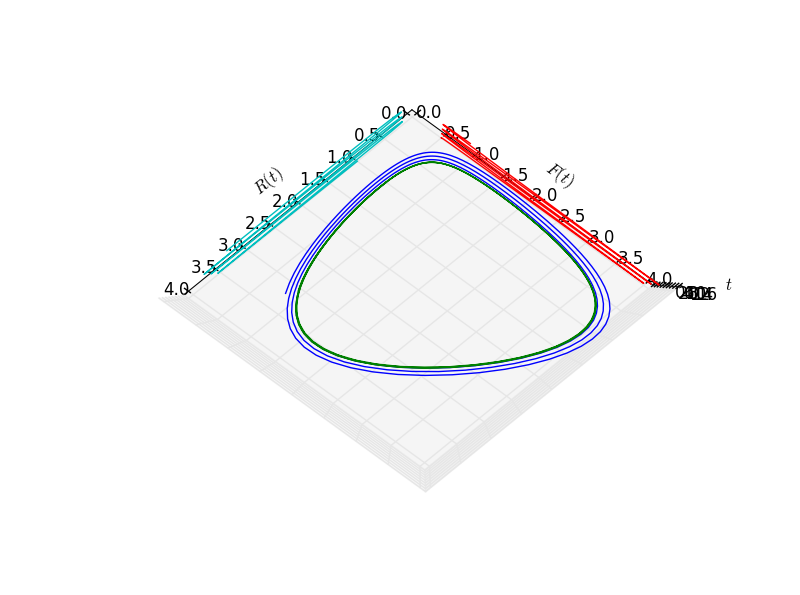
换一个角度看$$R(t),F(t)$$随$$t$$的变化

本节开头引入的弹簧-重物系统$$m\frac{d^2y}{dt^2} + ky = 0$$虽然是一个单一的二阶微分方程，但是如果我们引入$$\frac{dy}{dt} = v$$便可获得一个微分方程组：

$$\frac{dy}{dt} = v$$

$$\frac{dv}{dt} = -\frac{k}{m}y$$ 成为一个一阶方程组，这种方法称为降阶法。

弹簧-重物系统与我们的捕猎系统不同的一点在于：我们可以找到弹簧-重物系统的公式解，而无法找出捕猎系统的公式解。 考虑一个特殊情况，令$$k=m$$，则弹簧-重物系统简化为：

$$\frac{dy}{dt} = v$$

$$\frac{dv}{dt} = -y$$ 下面这些函数都是该系统的解之一

$$y_1(t)=sint, y_2(t)=2sint, y_3(t)=cost$$