9 线性微分方程
9.1 线性(linearity)
例子
考虑如下问题:
一个容积$$200$$升的容器中有$$100$$升盐水,盐的含量为$$1000$$克。假设盐浓度$$35$$克每升的盐水以每分钟$$4$$升的速度注入容器,完全混合的溶液以每分钟$$2$$升的速度流出。
用微分方程描述该容器内盐的含量,则盐含量的变化率为盐流入的速率减去盐流出的速率:
$$\frac{ds}{dt}= 35\times 4 - 2\frac{s}{100+(4-2)t}\ \qquad = 140 - \frac{s}{50+t}$$
加上$$s(0)=1000$$,我们便获得了一个初值问题。
本节内容便是讨论如何解这一类的微分方程。
线性微分方程
我们称一阶微分方程$$\frac{dy}{dt}=f(t,y)$$是线性的,如果其可以写成如下形式:
$$\frac{dy}{dt}=a(t)y+b(t)$$
即右边能写成因变量(这里是$$y$$)的线性函数的形式。
齐次与非齐次
对于线性微分方程,又分两大类:
- 齐次(homogeneous),$$b(t)=0$$
- 非齐次(nonhomogeneous),$$b(t)\neq 0$$
例如:
- 线性且齐次:$$\frac{dy}{dt}=(cost)y$$
- 线性非齐次:$$\frac{dy}{dt}=y-t^2$$
- 非线性: $$\frac{dy}{dt}=y^2$$
我们上面获得的盐水问题就是线性非齐次的。
线性齐次=可分
注意到线性齐次微分方程式是我们之前所提到的可分微分方程,可以通过两边同除以$$y$$后同时积分的方法来求解。
$$\frac{dy}{dt}=a(t)y\ \frac{1}{y}\frac{dy}{dt}=a(t)\ \int \frac{1}{y}dy = \int a(t)dt$$
看一个具体的线性齐次微分方程的例子:
$$\frac{dy}{dt}=\frac{-ty}{1+t^2}\ \frac{1}{y} \frac{dy}{dt} = \frac{-t}{1+t^2} \ \int \frac{1}{y} dy = \int \frac{-t}{1+t^2} dt \ ln(y) = -\frac{1}{2}ln(1+t^2) + C\ ln(y) = ln(\frac{1}{1+t^2}) + C\ y = (\frac{1}{\sqrt{1+t^2}})(e^C)\ y = (\frac{1}{\sqrt{1+t^2}})(C)\ y(t) = \frac{C}{\sqrt{1+t^2}}$$
斜率场和若干个解的图如:
tdomain = np.linspace(-3,3,30)
ydomain = np.linspace(-5,5,30)
y = Function('y')
formula = -1*t*y(t)/(1+t**2)
fg = plotSlopeField(tdomain,ydoman,formula,[(0,4),(0,3),(0,2),(0,1),(0,-1),(0,-2),(0,-3),(0,-4)])
fg.show()

可以看出其各个解之间的差距只是$$k$$值得不同。如果获得了一个解,便可以通过乘以一个值得方法来获得任何一个其他解。
齐次微分方程的线性原理(The Linearity Principle for Homogeneous Equations)
如果$$y_h(t)$$是一个齐次线性微分方程$$\frac{dy}{dt}=a(t)y$$的解,那么将其乘以任何一个常数$$k$$获得的$$y_k(t)=ky_h(t)$$也同样是一个解。
检该原理非常简单:
$$\frac{dy_k}{dt}=k(\frac{dy_h}{dt})\ \qquad = k(a(t)y_h)\ \qquad = a(t)(ky_h)\ \qquad = a(t)(y_k(t))$$
一阶方程的扩展线性原理(The Extended Linearity Principle for First-Order Equations)
考虑一个一阶非齐次线性方程(NHE):
$$\frac{dy}{dt}=a(t)y + b(t)$$
以及其对应的齐次方程(AHE):
$$\frac{dy}{dt}=a(t)y$$
- 如果$$y_h(t)$$是齐次方程的任意一个解,而$$y_p(t)$$是相应的非齐次方程的任意一个解,那么$$y_h(t)+y_p(t)$$也是该非齐次方程的一个解。
- 若$$y_h(t)$$和$$y_p(t)$$分别是非齐次方程的两个解,那么$$y_h(t)-y_p(t)$$是相应齐次方程的一个解。
因此,如果$$y_h(t)$$和$$y_p(t)$$分别是NHE和AHE的两个一般解,且$$y_h(t)$$非零,则$$ky_h(t)+y_p(t)$$是非齐次方程的一般解。
即:
一个非齐次线性方程的一般解可由(非齐次方程的任意一个解)和(相应齐次方程的一般解)相加获得
例子,非齐次线性方程:
$$\frac{dy}{dt}=\frac{-ty}{1+t^2}+\frac{2t^2+1}{4t^2+4}$$
现在知道其有一个特殊解$$y_p(t)=\frac{t}{4}$$
通过上面,我们已经知道对应的齐次线性方程的一般解为:
$$y(t) = \frac{C}{\sqrt{1+t^2}}$$
因此上述非齐次方程的其一般解为:
$$y(t) = \frac{t}{4} + \frac{C}{\sqrt{1+t^2}}$$
from sympy.abc import C
formula = -1*t*y(t)/(1+t**2) + (2*t**2+1)/(4*t**2+4)
solutions = t/4+C/(1+t**2)**0.5
points = [(0,4),(0,3),(0,2),(0,1),(0,-1),(0,-2),(0,-3),(0,-4)]
fig = plt.figure(num=1)
# create grid
T,Y = np.meshgrid(tdomain,ydomain )
# calculate slope vectors
U = 1
V = np.array([[formula.subs({y(t): yval, t: tval}) for tval in tdomain] for yval in ydomain],dtype = 'float')
N = np.sqrt(U**2+V**2)
U2, V2 = U/N, V/N
# make the plot
plt.quiver( T,Y,U2, V2)
plt.xlabel(r"$t$")
plt.ylabel(r"$y$")
plt.axhline(0,0,1,linewidth = 2, color = 'black')
plt.axvline(0,0,1,linewidth = 2, color = 'black')
for p in points:
Cval = solve(Eq(solutions.subs(t,p[0]),p[1]))[0]
solution = solutions.subs(C,Cval)
plt.plot(tdomain, np.array([solution.subs(t,tval) for tval in tdomain],dtype= 'float'),
linewidth = '2')
# limiting the axes
plt.xlim([tdomain[0],tdomain[-1]])
plt.ylim([ydomain[0],ydomain[-1]])
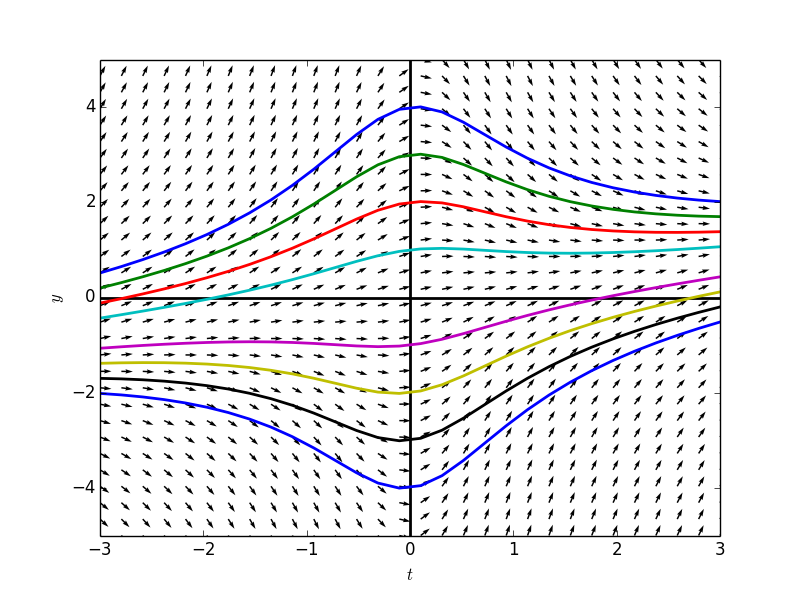
这个非齐次的线性方程的斜率场和解,可以看成是对应的齐次线性方程斜率场合解调整后的结果。
例题: 若已知$$y_p(t)=\frac{a}{t^2}$$是微分方程$$\frac{dy}{dt}=2ty-\frac{6}{t^2}-\frac{6}{t^3}$$的一个特殊解,(1)求$$a$$的值,(2)求方程的一般解,(3)求$$y(1)=3+2e$$初值问题的解。
(1):
$$\frac{dy_p(t)}{dt}=\frac{d}{dt}\frac{a}{t^2}\ \qquad = -2at^{-3}$$
$$\frac{dy}{dt}=2ty-\frac{6}{t^2}-\frac{6}{t^3}\ \qquad = 2t\frac{a}{t^2}-\frac{6}{t^2}-\frac{6}{t^3}\ \qquad = \frac{2a-6}{t}-\frac{6}{t^3}$$
因此有:$$\frac{2a-6}{t}-\frac{6}{t^3}= -2at^{-3}$$ 求解出:$$a=3$$
因此得到非齐次线性方程的一个一般解:$$\frac{3}{t^2}$$
(2): 对应的齐次线性方程为:$$\frac{dy}{dt}=2ty$$
用分离变量法不难求得其一般解为:$$Ce^{t^2}$$
因此非齐次方程的一般解为:$$y(t)=y_p(t)+y_h(t)=\frac{3}{t^2}+Ce^{t^2}$$
(3) 带入初值到一般解中,求出$$C=2$$,因此初值问题解为:$$y(t)=\frac{3}{t^2}+2e^{t^2}$$
9.2 猜解法
对于一个给定的非齐次线性方程,通过如下方法求解一般解:
- 解对应的齐次线性方程
- 猜测出非齐次方程的一个特殊解
- 将两者相加获得非齐次线性方程的一般解
例子:
$$\frac{dy}{dt}= -2y+3e^{-t/2}$$
对应的齐次方程为:
$$\frac{dy}{dt}=-2y$$
其一般解为:$$y(t)=Ce^{-2t}$$
对非齐次方程进行变换
$$\frac{dy}{dt}+2y=3e^{-\frac{t}{2}}$$ 考虑什么函数求导后加上2倍的本身可以获得$$3e^{-\frac{t}{2}}$$
猜测:$$y_p=\alpha e^{-t/2}$$
$$\frac{dy_p}{dt}+2y_p\
\qquad = -\frac{\alpha}{2}e^{-\frac{t}{2}}+2\alpha e^{-\frac{t}{2}}\
\qquad = \frac{3}{2}\alpha e^{-\frac{t}{2}}$$
在$$\alpha = 2$$时,$$y_p(t)= 2e^{-\frac{t}{2}}$$为非齐次方程的一个特殊解,因此获得一般解为:
$$y(t)=2e^{-\frac{t}{2}}+Ce^{-2t}$$
看一看方程的解和斜率场,洋红色的一条线代表的是上面我们求出的特殊解,注意到所有的解在随着$$t\rightarrow \infty$$时,都在趋近于我们求出来的特殊解:
tdomain = np.linspace(-3,3,30)
ydomain = np.linspace(-2,8,30)
formula = -2*y(t)+3*sympy.E**(-1*t/2)
fg = plotSlopeField(tdomain,ydomain,formula,[(0,0),(-1,0),(-2,0),(-3,0),(0,2),(0,3)])
fg.show()

例子2:
$$\frac{dy}{dt}=-y+2cos(4t)$$
对应齐次方程的一般解为:$$y_h(t)=Ce^{-t}$$
猜测:$$y_p = \alpha cos4t + \beta sin4t$$
$$\frac{y_p}{t}+y\
\qquad = 4\alpha sin4t -4\beta cos4t + \alpha cos4t + \beta sin4t\
\qquad = (4\alpha + \beta)sin4t + (\alpha - 4\beta)cos4t$$
要使得其等于$$2cos4t$$,获得方程组:
$$\begin{cases} 4\alpha+\beta = 0\ \alpha-4\beta =2 \end{cases}\ \implies\ \begin{cases} \alpha = \frac{2}{17} \ \beta = \frac{8}{17} \end{cases}$$ 因此获得非齐次方程的特殊解:
$$y_p(t) = \frac{2}{17}cos4t + \frac{8}{17}sin4t$$
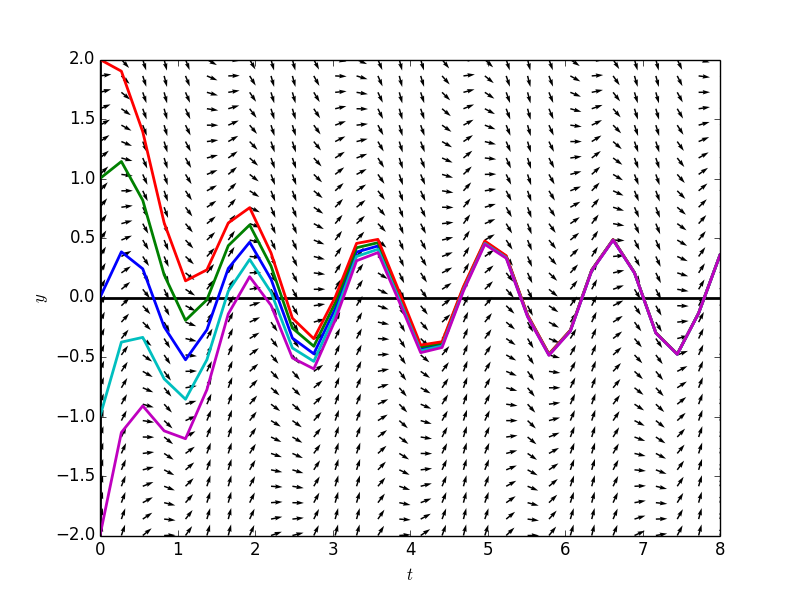
方程的一般解为:
$$y(t)=\frac{2}{17}cos4t + \frac{8}{17}sin4t+Ce^{-t}$$
看一看方程的解和斜率场,蓝色的一条线代表的是上面我们求出的特殊解,注意到所有的解在随着$$t\rightarrow \infty$$时,都在趋近于我们求出来的特殊解,因此这个特殊解又称为稳态解(steady state solution):
tdomain = np.linspace(-3,3,30)
ydomain = np.linspace(-2,8,30)
formula = -2*y(t)+3*sympy.E**(-1*t/2)
fg = plotSlopeField(tdomain,ydomain,formula,[(0,0),(-1,0),(-2,0),(-3,0),(0,2),(0,3)])
fg.show()
例子3:
$$\frac{dy}{dt}=-3y+2e^{-3t}$$
相应齐次方程的一般解为:$$Ce^{-3t}$$
猜测$$y_p(t)=\alpha e^{-3t}$$,将不会有效果,我们永远不应该猜测齐次方程的解为对应非齐次方程的解。
而是猜测:$$y_p(t)=\alpha t e^{-3t}$$
$$\frac{dy_p}{dt}+3y_p = \alpha (e^{-3t}-3te^{-3t}) + 3\alpha t e^{-3t}\ \qquad = \alpha e^{-3t}$$ 要其为$$2e^{-3t}$$,则需要$$\alpha = 2$$
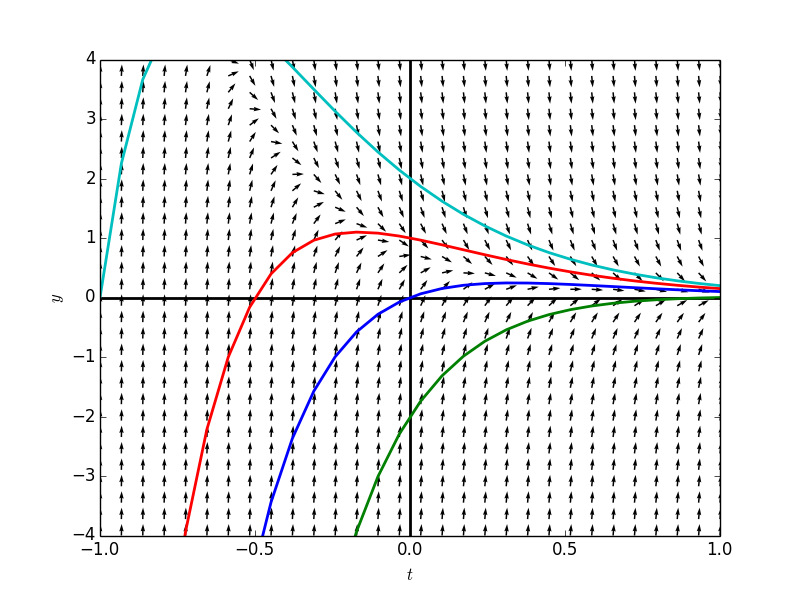
因此特殊解为:$$y_p(t) = 2te^{-3t}$$
一般解为:$$(k+2t)e^{-3t}$$
同样看看图:
tdomain = np.linspace(-1,1,30)
ydomain = np.linspace(-4,4,30)
formula = -3*y(t)+2*sympy.E**(-3*t)
fg = plotSlopeField(tdomain,ydomain,formula,[(0,0),(0,-2),(0,1),(0,2)])
9.3 神奇函数(积分因子 integrating factor)
将非齐次方程$$\frac{dy}{dt}=a(t)y+b(t)$$进行改写为$$\frac{dy}{dt}+g(t)y=b(t)$$
即,令$$g(t) = -a(t)$$
注意到,此时微分方程的左边$$\frac{dy}{dt}+g(t)y$$"看上去像"是用乘积法则求导后的结果。
我们希望找到一个函数$$\mu (t)$$使得$$\mu (t) (\frac{dy}{dt} + g(t)y) = \frac{d}{dt}(\mu(t)y)$$能够成立。
$$\mu (t)\frac{dy}{dt} + \mu (t) g(t)y = \mu (t) \frac{dy}{dt} + \frac{d\mu}{dt}y\
\frac{d\mu}{dt} = \mu (t) g(t)\
\frac{d\mu}{dt} = g(t) \mu$$
得到一个线性的齐次方程
其解为$$\mu (t) = ke^{\int g(t)dt}$$,因为我们只需要任意一个解就可以了,令$$k=1$$获得一个满足条件的函数$$\mu (t) = e^{\int g(t)dt}$$
在原方程两边同时乘以$$\mu (t)$$,便可以求解了。
方法小结:
- 给定一个非齐次微分方程:$$\frac{dy}{dt}+g(t)y = b(t)$$
- 令积分因子为:$$\mu (t) = e^{\int g(t)dt}$$
- 方程两边同时乘以积分因子获得:$$\frac{d}{dt}(\mu (t)y)=\mu (t)b(t)$$
- 两边同时针对$$t$$进行积分:$$\mu (t)y = \int \mu(t)b(t)dt$$
例子:
方程:$$\frac{dy}{dt}= \frac{y}{t}+tcost$$
积分因子为:$$\mu (t) = e^{\int -\frac{1}{t}dt} = e^{-ln(t)} = e^{ln(\frac{1}{t})}=\frac{1}{t}$$
两边同乘积分因子:
$$\frac{1}{t}\frac{dy}{dt} - \frac{1}{t} \frac{y}{t} = cost\ \frac{1}{t}(\frac{dy}{dt}) - \frac{1}{t^2}y = cost\ \frac{d}{dt}(\frac{1}{t}y)=cost$$
两边同时积分:
$$\frac{1}{t}y = sint + k\ y(t) = tsint + kt$$
formula = y(t)/t+t*sympy.cos(t)
tdomain = np.linspace(-10,10,30)
ydomain = np.linspace(-30,30,30)
fg = plotSlopeField(tdomain,ydomain,formula,[(math.pi/2.0,math.pi/2.0),(math.pi/2.0,math.pi),(math.pi/2.0,0)])
从上到下分别为$$k = 1, k = 0, k = -1$$的解

回到本节开始时候的方程:
$$\frac{ds}{dt}= 140 - \frac{s}{50+t},\qquad s(0) = 1000$$
$$\frac{ds}{dt} + \frac{s}{50+t} = 140$$
积分因子为:
$$\mu(t) = e^{\int \frac{1}{50+t}dt} = e^{ln(50+t)} = 50+t$$
方程两边同时乘以积分因子:
$$(50+t)\frac{ds}{dt} + s = 140(50+t)\ \frac{d}{dt}((50+t)s) = 140(50+t)$$ 两边同时积分:
$$(50+t)s = 7000t + 70t^2 + k$$ 将$$s(0) = 1000$$带入上式获得$$k = 50000$$
得到最终解:
$$s = \frac{7000t + 70t^2+50000}{50+t}$$