阻尼谐振(Damped Harmonic Oscillation)

为我们之前提到的弹簧-重物系统增加上阻力。

前提假设：

• 阻力与重物的速度成正比: $$F_d = -b\frac{dy}{dt}, b > 0$$
• 牛顿第二定律：$$F=ma$$
• 胡克定律： $$F_s = -ky$$

变量：

1. 自变量：$$t$$ 时间
2. 因变量：$$y$$ 位移

获得阻尼振动的方程为：

$$F_s + F_d = F = ma = m \frac{d^2y}{dt^2}\ -ky -b\frac{dy}{dt} = m \frac{d^2y}{dt^2} \ m\frac{d^2y}{dt^2} + b\frac{dy}{dt} +ky = 0$$

可以令$$v = \frac{dy}{dt}$$，将上面方程降为一个一阶方程组：

$$\begin{cases} \frac{dy}{dt} = v \ \frac{dv}{dt} = -\frac{k}{m}y - \frac{b}{m}v \end{cases}$$

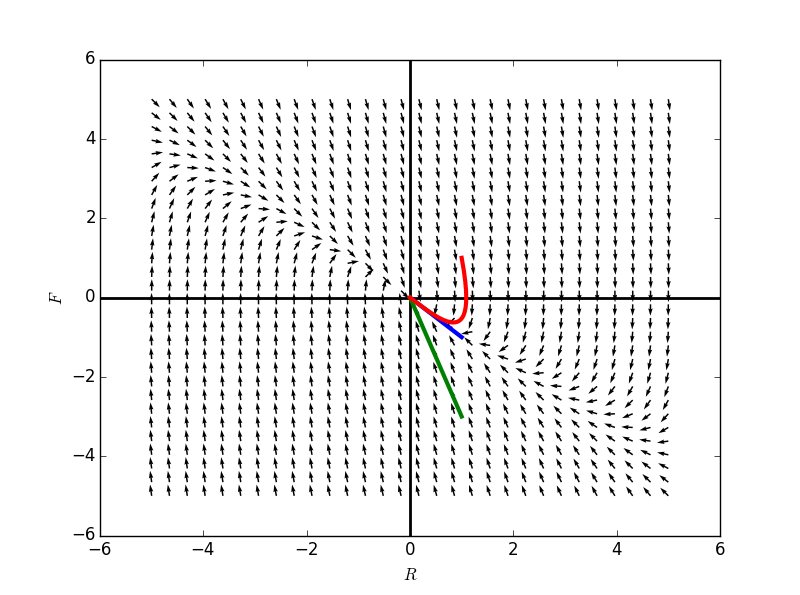
给定一个初始的位置$$y=3$$，令$$k,m$$不变，调节$$b$$值，看解的不同表现：

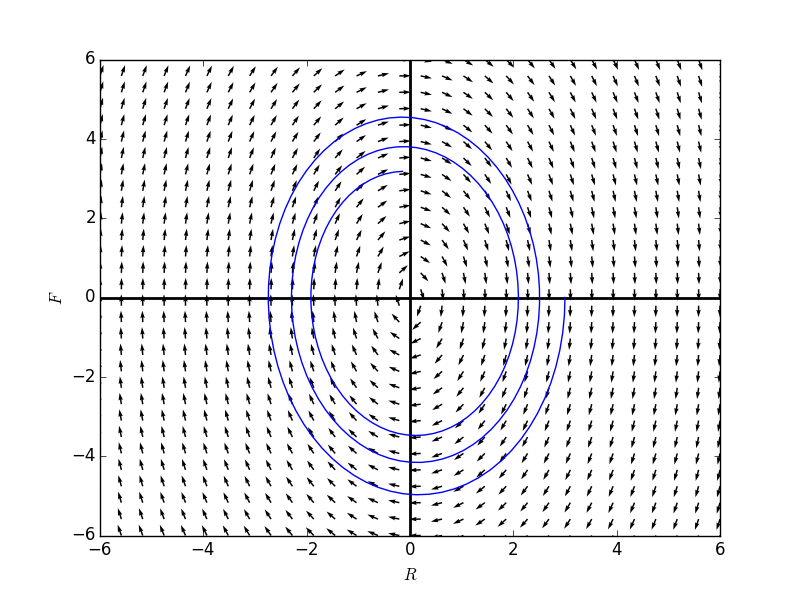
当$$b = 0$$时，没有阻力：

    R = Function('R')
    F = Function('F')

    formulaR = F(t)
    formulaF = -3*R(t)

    Rdomain = np.linspace(-6,6,30)
    Fdomain = np.linspace(-6,6,30)

    fg1 = directionField(formulaR, formulaF,Rdomain, Fdomain)
    Tvals,Rvals,Fvals = numericalApproxForTwo(formulaR, formulaF, 3.0, 0.0, dt = 0.0005, steps = 20000)
    plt.plot(Rvals, Fvals)
    fg1.show()

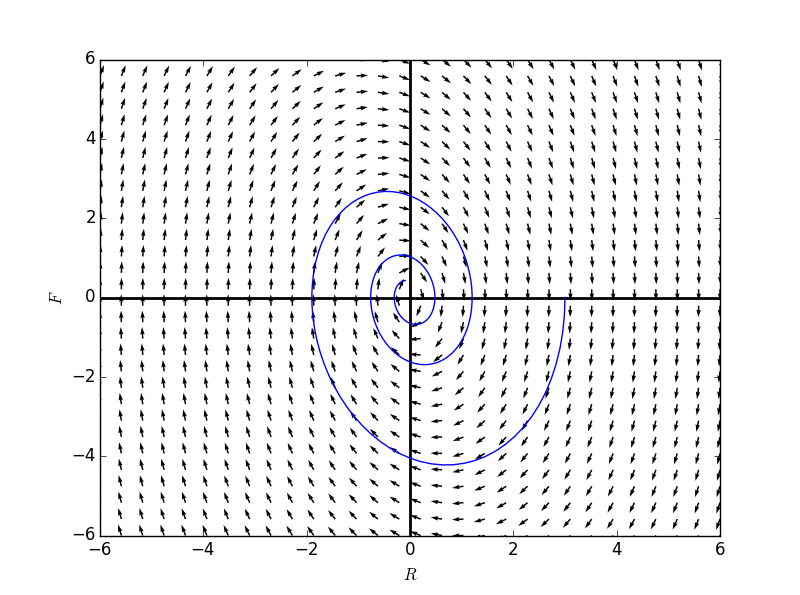
    R = Function('R')
    F = Function('F')

    formulaR = F(t)
    formulaF = -3*R(t) - 0.1*F(t)

    Rdomain = np.linspace(-6,6,30)
    Fdomain = np.linspace(-6,6,30)

    fg2 = directionField(formulaR, formulaF,Rdomain, Fdomain)
    Tvals,Rvals,Fvals = numericalApproxForTwo(formulaR, formulaF, 3.0, 0.0, dt = 0.0005, steps = 20000)
    plt.plot(Rvals, Fvals)
    fg2.show()

    R = Function('R')
    F = Function('F')

    formulaR = F(t)
    formulaF = -3*R(t) - 0.1*F(t)

    Rdomain = np.linspace(-6,6,30)
    Fdomain = np.linspace(-6,6,30)

    fg2 = directionField(formulaR, formulaF,Rdomain, Fdomain)
    Tvals,Rvals,Fvals = numericalApproxForTwo(formulaR, formulaF, 3.0, 0.0, dt = 0.0005, steps = 20000)
    plt.plot(Rvals, Fvals)
    fg2.show()

猜测阻尼振动的一般解

$$ m\frac{d^2y}{dt^2} + b\frac{dy}{dt} +ky = 0$$

猜测$$y(t) = e^{\lambda t}$$,其中$$\lambda$$是一个需要计算得出的常数。

$$\frac{dy}{dt} = \lambda e^{\lambda t}$$

$$\frac{d^2y}{dt^2} = {\lambda}^2 e^{\lambda t}$$

带入方程获得：

$$m({\lambda}^2 e^{\lambda t}) + b(\lambda e^{\lambda t}) + k e^{\lambda t} = 0 \ (m{\lambda}^2 + b\lambda +k) e^{\lambda t} = 0$$

左边是一个多项式乘以$$e^{\lambda t}$$，该多项式被称为特征多项式(characteristic polynomial)

因为我们关注的是$$\lambda$$取值为多少能使得该多项式取值为$$0$$，因此又称$$m{\lambda}^2 + b\lambda +k = 0$$为特征方程。

例子：$$m = 1,b = 3,k = 2$$

$$\frac{d^2y}{dt^2} + 3\frac{dy}{dt} + 2y = 0$$ 特征方程为：

$${\lambda}^2 + 3\lambda + 2 = 0$$ 解为：

$$\begin{cases} \lambda = -2 \ \lambda = -1 \end{cases}$$

因此获得原方程的两组解：

$$\begin{cases} y_1(t) = e^{-2t} \ v_1(t) = -2e^{-2t}\end{cases}$$

$$\begin{cases} y_2(t) = e^{-t} \ v_2(t) = -e^{-t}\end{cases}$$

写成向量函数的形式为：

$$Y_1(t) = \begin{pmatrix} e^{-2t} \ -2e^{-2t} \end{pmatrix}$$ 对应初值为：

$$ Y_1(0) = \begin{pmatrix} 1 \ -2 \end{pmatrix}$$

$$Y_2(t) = \begin{pmatrix} e^{-t} \ -e^{-t} \end{pmatrix}$$ 对应初值为：

$$ Y_2(0) = \begin{pmatrix} 1 \ -1 \end{pmatrix}$$

下图中，有两个解对应于上面这两个，是哪两个？